New Paper - Accuracy of Inference
04/12/2017 - Jim Barrett
A couple of weeks ago I put my newest paper on to the arXiv, which you can find here; https://arxiv.org/abs/1711.06287
The paper describes how much we can hope to learn from gravitational-wave observations of black holes, focusing in particular on how well we can constrain our models of the evolution of binary stars. In order to calculate this I used COMPAS, the binary evolution simulation software we are developing here in Birmingham, and a technique called Fisher information matrices.
If you have a model, which depends on some parameters , and makes predictions about some observable random variable, then the Fisher information quantifies how sensitive the expected observations are to changes in the underlying parameters. If some parameters have a large effect on our expected observations, then it makes sense that we can learn a lot about them.
I calculated the Fisher matrix by running COMPAS (a lot!) and seeing how the output changed with respect to four different bits of physics; the strength of supernova kicks, the ferocity of stellar winds during two different stellar evolutionary phases, and the frictional energetics during the common envelope phase. Below is the money plot from the paper.
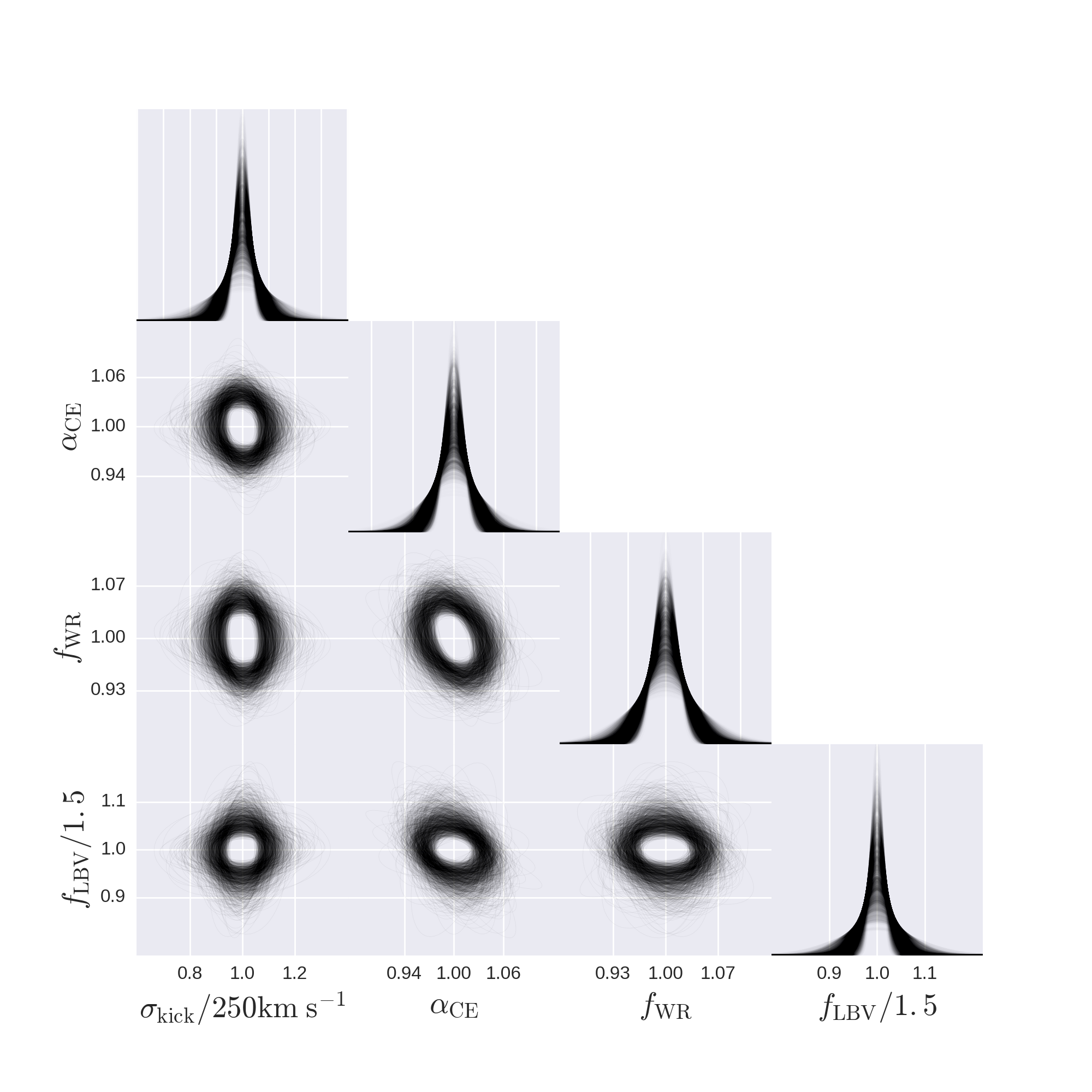
The plot shows how accurately we will be able to measure each of these parameters after 1000 observations of binary black holes. The fuzziness comes from a quantification of the various sources of uncertainty in this process. It also shows how the different parameters behave with respect to each other (their correlation). The way I like to think about this plot is in terms of null hypothesis testing. If we find the truth is a massive outlier with respect to these distributions, then we reject the null hypothesis that our model is correct. This plot shows that the model doesn't have to be wrong by more than a few percent before we can rule out our model.